[시계열 데이터를 이미지화하기] Gramian Angular Field(GAF) Imaging 개념이해

Gramian Angular Field (GAF) 개요

• 시계열 데이터를 비-데카르트 좌표계(non-Cartesian coordinates system)의 이미지로 표현한 것
• 데카르트 좌표계를 사용하지 않는 대신에, 각각의 좌표 값들은 극좌표계(Polar Ordinate system)의 방식으로 계산됨
• 이로 인해, 각 시점의 시간적 상관관계(temporal correlation)를 표현 가능
• GAF는 왼쪽 상단에서 오른쪽 하단으로 이동함에 따라 시간이 증가하기 때문에 시간 종속성을 보존한다
• 주대각선은 원시 데이터의 값과 각도 정보를 포함하기 때문에 이를 이용하여 원시 데이터를 복구할 수 있다
• 따라서, 변환된 이미지는 왼쪽 위(top-left)에서 오른쪽 아래(bottom-right) 방향으로 원 시계열에 대응되며, 이미지는 가운데 대각선을 기준으로 대칭이다

 

* 데카르트 좌표계(Cartesian coordinates system): X축, Y축 등의 수직 축 기반의 좌표계

* 극좌표계(Polar Ordinate system): 평면 위의 위치를 각도와 거리를 써서 나타내는 2차원 좌표계

 

데카르트 좌표계 (Cartesian coordinates system)

극좌표계 (Polar Ordinate system)

 

 

 

0. 사전 지식

Gramian Angular Field를 온전히 이해하기 위해서는 inner product(내적)와 Gram Matrix(그람 행렬)에 대한 이해가 필수적이다

2021.07.14 - [Data Science] - 내적(inner product, dot product, scalar product, projection product) 개념 이해

2021.07.14 - [Data Science] - Gram Matrix (그람 행렬) 개념 이해

 

 

1. 변환 과정

Gramina Angular Field (GAF)는 시계열 데이터를 matrix로 변환시키기 위해 2가지 단계를 거친다

 

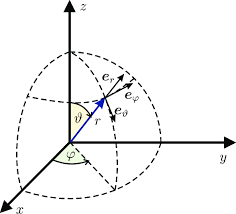
1)      공간 좌표계(time x value)의 값을 극좌표계의 값으로 변환시킨다

극좌표계 값으로 변환시킬 때, 다음의 수식이 계산된다

 

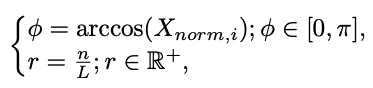
• 여기서 L은 시간 차원(temporal dimension)을 scaling하지만 final matrix에는 영향을 미치지 않는다.
• 이 변환은 bijective(두 집합 사이를 중복없이 모두 일대일로 대응시키는 것)이며, 절대적인 시간 관계는 유지된다.
• 위 수식은 [-1,1] 사이 범위에서만 적용되기 때문에, 해당 수식을 대입하기 전에 데이터를 먼저 min-max scaling해주는 과정이 필요하다.

 

2)      극좌표계의 Gramian matrix가 계산됨

 

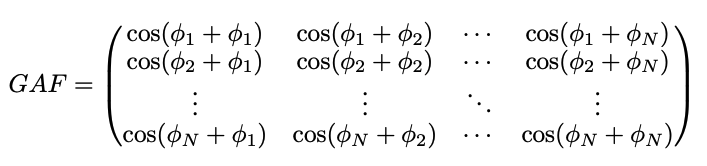
• 내적 연산(inner product)를 사용하는 Gram matrix와 유사하기 때문에, Gramian matrix로 이름이 붙여졌다
• 하지만, cos(xi + xj) 는 (정확히 내적의 연산과 동일하지는 않기 때문에) 내적의 모든 조건을 만족하지 않는다. (왜 동일하지 않은지는 위 내적에 대한 기본 이해를 하면 알 수 있다)
• 게다가, 행렬은 r값에 의존적이지 않기 때문에 시간과 극좌표계로 변환시 사용하는 L값에도 영향을 받지 않는다.
• 즉, GAF 변환은 이미지로 변환시킨 이후에 다시 시계열로 되돌릴 수 없다(reverse transformation이 불가하다)는 한계가 있다.
• 이는 곧 이미지 변환이 되면 정보의 손실(loss of information)을 발생시키게 되지만, inverse space에서 moderate한 overlap만 있기 때문에 input값이 무엇이었는지에 대한 대략적인 유추가 가능하다.

 

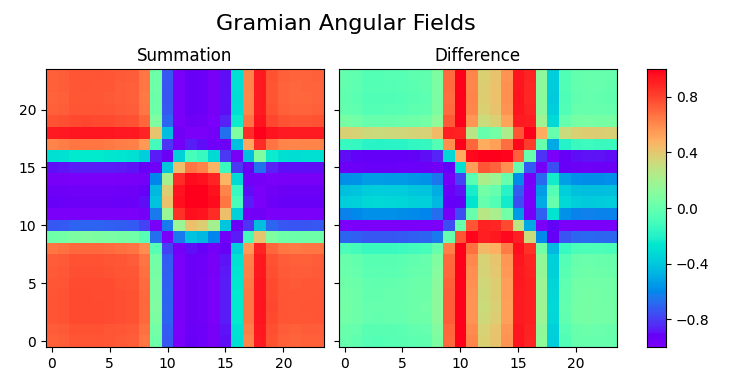
2. GAF 기법의 2가지 분류 (GASF, GADF)

• GAF기법은 사용되는 삼각함수/각도의 합과 차에 따라 GASF(Gramian Angular Summation Field)와 GADF(Gramian Angular Difference Field ) 2가지로 나뉜다
• GASF는 cosine함수를 사용하며, GADF는 sine함수를 사용한다

1)       Garamian angular summation field (GASF)는 i와 j의 시간쌍으로 이루어진 극좌표계 시계열 데이터의 각도의 합으로 나타낸다

2)      Gramian angular difference fIeld(GADF)는 GASF와 반대로 극좌표계의 각도의 차로 다음과 같이 정의한다

 

 

3. 사용 가능한 모듈

• 파이썬 pyts(Python Package for Time Series Classification) 모듈 사용 가능

Gramian Angular Field — pyts 0.11.0 documentation

 

Reference

Encoding time series as images