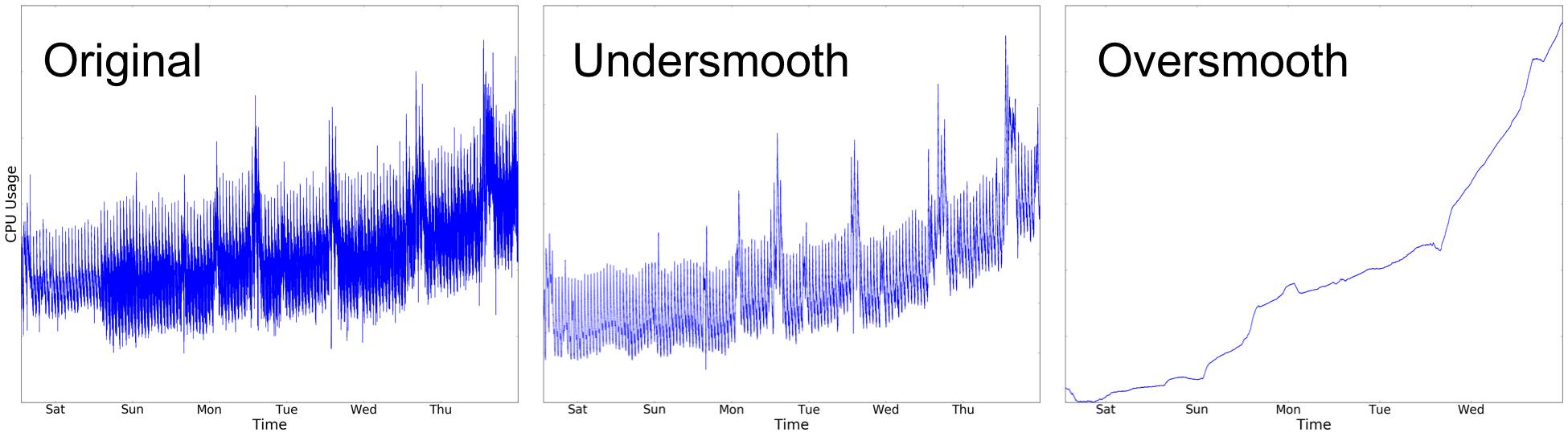
데이터 평활을 수행하는 데는 다양한 이유가 있고, 현실의 시계열 데이터는 분석 전에 평활되는 것이 보통
특히 데이터를 쉽게 이해하는 목적으로 시각화 자료를 만들기 위해 평활을 진행하는 경우가 있음
1. 평활이란?
시간에 따라 수집된 시계열 데이터에는 무작위적인 변화량이 있다. 평활(Smoothing)이란, 이렇게 무작위적 변화로 생기는 효과를 줄이는 방법들 중 흔히 사용되는 기법 중 하나다.
예를 들어, 주어진 시계열 자료에 평균을 취하는 것은 가장 단순한 평활법이다. 하지만, 평균은 모든 과거 관측값을 동일한 가중치로 다루기 때문에, 추세(Trends)가 존재하는 경우 좋은 지표가 될 수 없다.
평활을 이용해 시계열을 세 가지 구성성분으로 분해하거나, 예측을 수행할 수 있다.
2. 평활의 목적
A. 데이터 준비
B. 특징 생성
C. 예측
D. 시각화
3. 지수평활 (exponential smoothing)
최근에 측정된 데이터에 가중치를 더 두고 싶을 때 사용
누락된 데이터를 주변 값의 평균으로 대치하는 이동평균과는 대조적으로, 지수평활은 좀 더 최근 데이터일수록 더 많은 가중치를 줘서 시간의 특성을 더 잘 인식할 수 있도록 만들어진 방법
pandas 팩키지의 ewma() 함수로 다양한 감쇠요인(decay factor)를 적용하여 쉽게 평활 가능
평활요인(smoothing factor)로도 불리는 alpha 파라미터의 값은 기존의 평균 정보를 유지하는 것에 비해 현재의 값을 얼마나 갱신해야 하는지에 대한 영향을 미친다(alpha 값이 작을수록 현재 값과 차이 나게 smoothing됨)
alpha 값이 크면 클수록 값의 갱신은 있는 그대로의 현재 값에 가깝도록 더 빨리 갱신된다
1) 단순 지수평활
장기적인 추세의 데이터에서는 단순한 지수평활이 예측을 잘 수행하지 못한다
2) 홀트(Holt)의 방법/ 홀트-윈터스(Holt-Winters)의 평활
추세를 가진 데이터와 추세 및 계절성을 모두 가진 데이터에 적용 가능한 지수평활법
3) 칼만 필터(Kalman Filter)
변동성 및 측정오차의 조합으로 시계열 과정을 모델링해 데이터를 평활
칼만 필터는 물체의 측정값에 확률적인 오차가 포함되고, 또한 물체의 특정 시점에서의 상태가 이전 시점의 상태와 선형적인 관계를 가지고 있는 경우 적용이 가능하다
잡음이 포함되어 있는 측정치를 바탕으로 선형 역학계의 상태를 추정하는 재귀 필터
이때, 칼만 필터가 재귀 필터란 말은, 칼만 필터는 바로 이전 시간에 추정한 값을 토대로 해서 현재의 값을 추정하며, 바로 이전 시간 외의 측정값이나 추정값은 사용하지 않는다는 것을 의미한다
시간 전후 데이터를 모두 고려하므로 사전 관찰을 주의해야함
4) LOESS (locally estimated scatterplot smoothing)
지역적으로 데이터를 평활하는 비모수적(non parametric) 방법
시간 전후 데이터를 모두 고려하므로 사전 관찰을 주의해야함


